A Generalization of Dilworth’s Decomposition Theorem for Partially Ordered Multisets

Abstract

Dilworth’s decomposition theorem characterizes the size of the largest antichain of any finite partially ordered set in terms of a partition of the order into a minimum number of chains. In this study, Dilworth’s theorem is generalized using multisets i.e., mathematical entities that admit repetition. The theorem is formulated analogously using a partially ordered multiset (or pomset), with combinatorial parameters defined in the multiset setting. Basic conditions are established for constructing antichains of an ordered multiset such that no two elements are comparable or equal. These conditions are adopted in proving Dilworth’s theorem in the multiset setting, showing that the smallest number of chains in a partition of a pomset coincides with the size of the largest subpomset containing incomparable elements. Lastly, an algorithm for recursively constructing antichains of an ordered multiset is formulated. Python programming language is used in implementing this algorithm on an ordered multiset structure. It is decidable and runs in quadratic time complexity 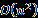. For any finite pomset, the number of antichains constructed via this algorithm is the same as the size of a maximum multiset chain in the pomse